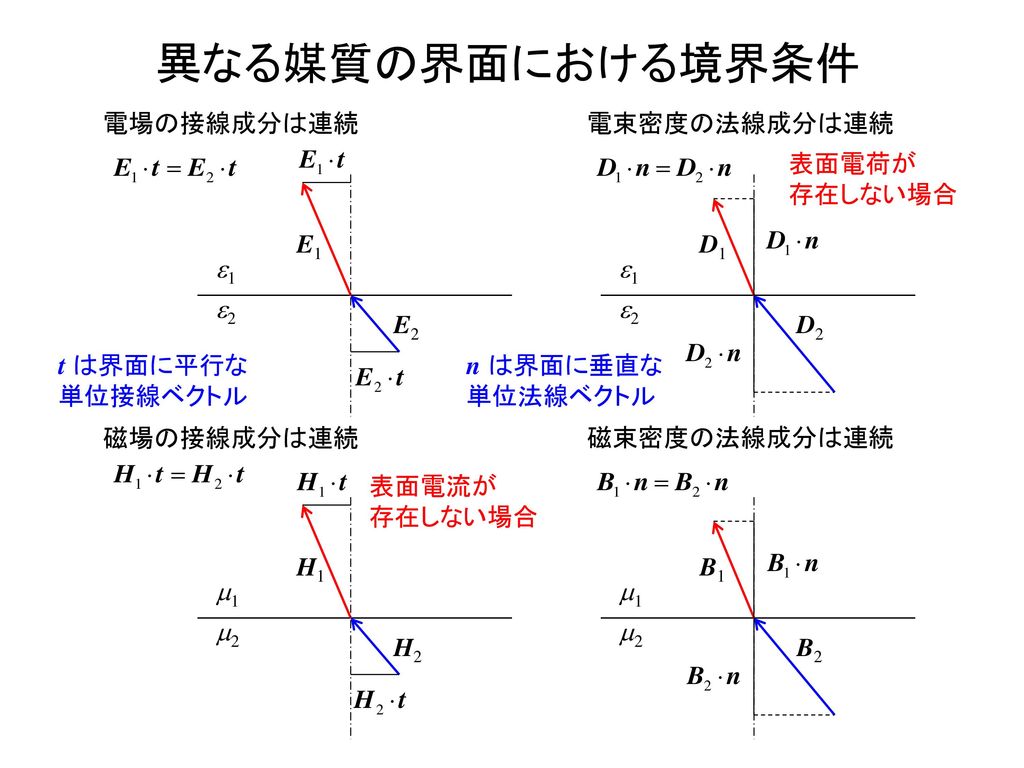
電場と磁場の境界条件より、境界面 y = 0 において、次の関係が成り立つ。 Einp Erp = Etp Binp Brp = Btp 参考 電場と磁場の境界条件 また、p偏光では電場はxy平面上で振動するから、 Einp, Erp, Etp をそれぞれx,y成分に分解できる。 境界面に対して平行な電場は連続であるという境界条件より、x成分の境界条件は次のように書き換えられる。 Einpcosθin − Erpcosθr =平行偏波(TMy or TMx モード) 斜入射の反射・透過解析 v26 May21 科 年 番 氏名 1 入射波の接線成分 Region1 x y z Ei Hi y=0 Region2 h1 h2 qi qr qt Er Hr Ht Et k1 k1 k2 k2sinqt k2k2cosqt k1sinqik1cosqi k1 k1cosqr k1 k1sinqr Ei icosq cosEr rq Et tcosq 図1 2 層媒質境界面y = 0 における入射・反射・透過の解析モ デル。入射電界の振幅本例題について 開放型コイルによる電磁共鳴型無線電力伝送の解析例を示します。 低周波解析用の開放境界(※1)を使用することで精度の向上を図ります。 表に記載されていない条件は初期設定の条件を使用します。
佚名 文革中的婚礼和证书 Cnd刊物和论坛
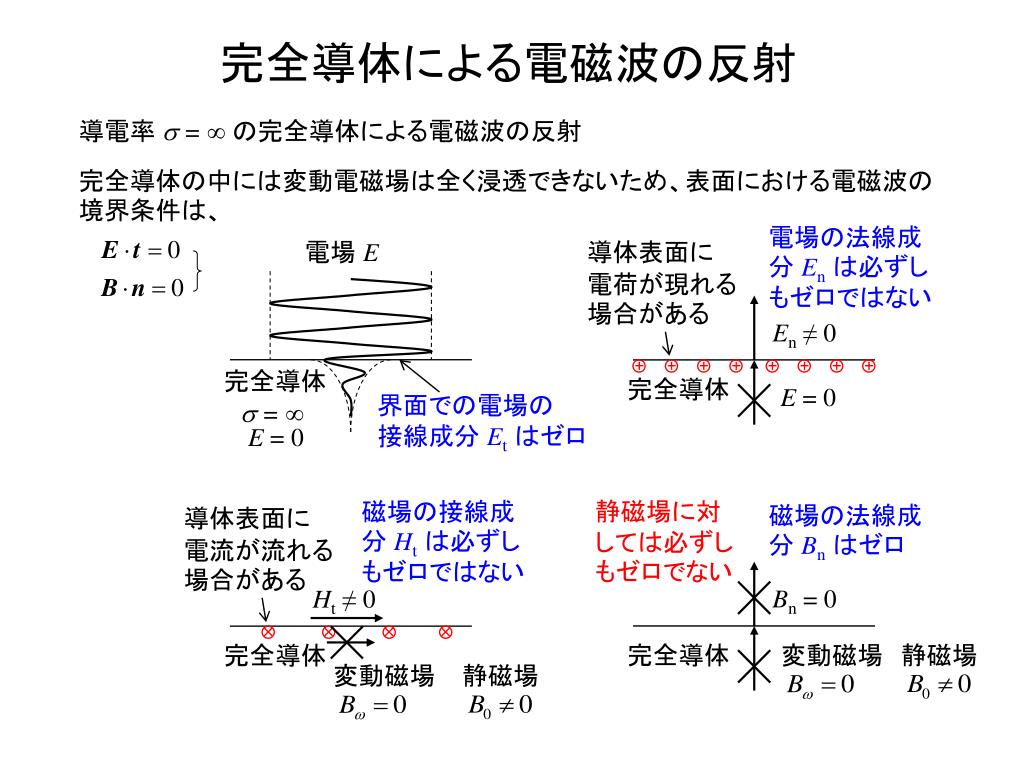
電磁波 完全導体 境界条件
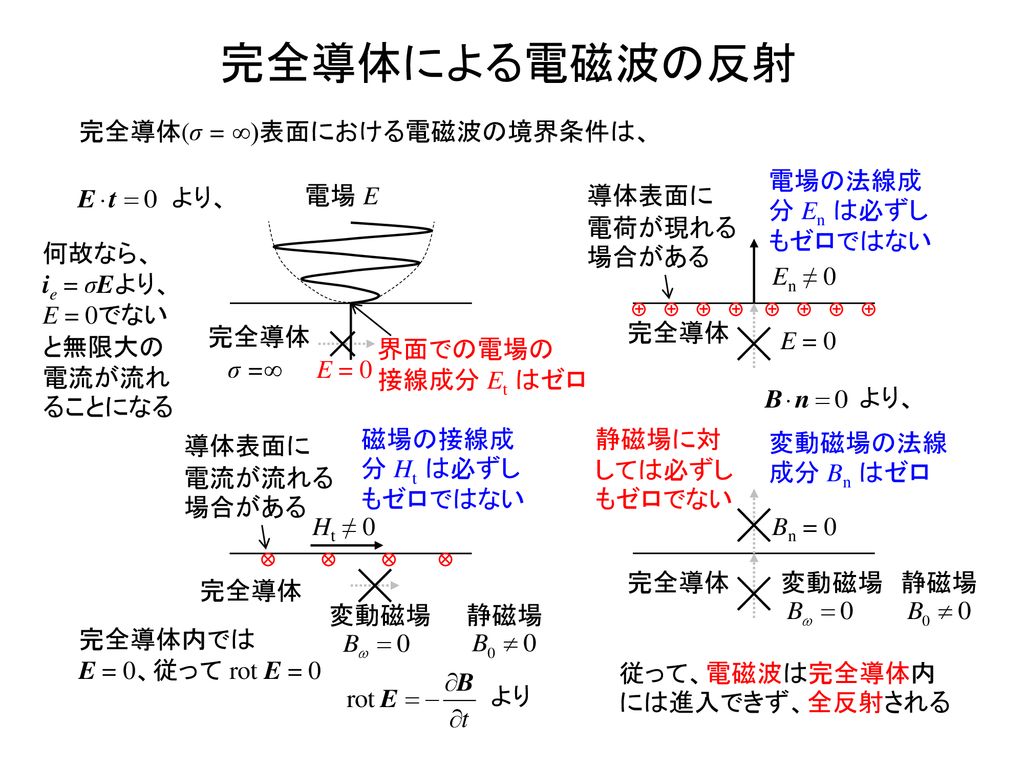
電磁波 完全導体 境界条件- point 波(電磁波・音波)が,異なる媒質の境界面に対し垂直に入射した場合の反射・透過について. 量子力学で,1次元の階段型ポテンシャルに平面波が入射したときの反射・透過について. これらの波動現象が,ほとんど同じ方法で扱えることを,計算を比較しながら確認する. その境界条件というのはマクスウェル方程式から導かれるのだが, 結論から言えばとても簡単である ・境界面に平行な電場成分は連続でなくてはならない ・境界面に平行な磁場成分は連続でなくてはならない ・境界面に垂直な電束密度成分は連続でなくてはならない ・境界面に垂直な磁束密度成分は連続でなくてはならない 連続だというのはつまり, 境界を挟んで向こうとこちら




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba
境界条件 rot t ∂ =− ∂ B E rot t ∂ = ∂ D HJ divB =0 divD =ρ 電磁界に関するすべて の性質はMaxwellの方 程式に記述されている。周期境界条件の導入による振幅の規格化 後の計算の便宜のため,周期境界条件を導入し,振幅を規格化する.空間を0 ≤ x ≤ L,0≤ y ≤ L,0≤ z ≤ L の立方体の集まりだと考え,電磁波はこの立方体を周期として周期的になっているとする.L が電磁波の波長よ11マ イクロ波空胴共振器 完全導体で囲まれた空胴内に存在する電磁波のふるま いは,マクスウェル方程式から導かれた下記の波動方程式 (1) (2) と,境界条件で記述されるこ こでEとHは 電界および磁堺 の強さ,cは光速である電界に関する境界条件はその接綜
平面波と境界条件 1 1st Lst v26 Jan21 電磁波における境界条件の使途 Region 1 Region 2 透過 (未知) 111 111 H jE E jH 222 222 H jE E jH 22 EkE1110 22 EkE21 11 1本章では,電磁界の基礎として,最初に,マクスウェル方程式(21 節),構成関係式(22 節),波動方程式と平面波(23 節)を説明する.次に,波源が存在する場合の放射に関する電磁波(光)の反射 電磁波の場合も,音波の圧力波・速度波の関係と同じ事情がある。同じ角振動数ωで振動す る電場ベクトルE と磁場ベクトルH は同位相で,波数ベクトルkに垂直な面内で互いに直交し, (E, H, k)で右手系を成している。このため,例えば垂直入反射を考えると,電場が反射で向き
電磁波伝搬を解析するときに、銅などの良導体を完全導体壁とすべきか、表面インピーダンス近似した境界条件を使用すべきかが気になった。 よって、完全導体壁と表面 インピーダンス 法を Maxwell 方程式から導出して、その違いを検討したい。この入射面を基準として,電界ベクトルが入射面内に平行な(横たわっている)場合 を平行偏波という.また,磁界が入射面に垂直なので TM (Transverse Magnetic)波とい う.さらに,境界面を地面にたとえると地面に対して垂直の場合に相当するので垂直偏 波,あるいはH 波と呼ぶこともある.図2参照. n θ E θ n E 垂直偏波,TM 波, H 波 水平偏波,TE 波, E 波 図2 偏波の名称 一方,電界ベク 界,あ るいは磁界は波の性質をもって空間を伝搬している ことになる。 電磁界解析では,上 記(3),(4)の方程式の組み合わせを 種々の境界条件のもとに解くことになる。 4、電磁界解析法 シミュレーションで使われる電磁界解析法は,大 きく分




有答案了吗 困扰天文学家多年的问题 宇宙之外还有什么 宇宙大爆炸 太阳 奇点 地球 网易订阅



電場輻射electromagnetic Fefvw
外部境界条件と重なるときはこちらが優先されます。 種類と境界条件名はユーザが設定できます。 外部境界条件 解析実行時にモデルの一番外側に設定されます。 外部境界条件の種類はユーザが選択できます。 境界条件は大きく3つに分けられます。 境界条件 それではs偏光の反射係数を求めて行きましょう。これは電磁波の境界条件から求めることができます。 境界を含む電場の周回積分は0 $$ \oint {\bf E} \cdot d{\bf r} = 0 $$ を使っていきます。 (「電磁気電磁気学III 第8講 3 (0) いま入射波の波数ベクトルのx成分はゼロであり、(86)から反射波および透過波の波数ベクトル のx成分はいずれもゼロだから、 (1) となる。したがって入射波、反射波および透過波の磁場成分は以下のようにあたえられる。




Wo19 号 電磁波伝搬制御部材 電磁波伝搬制御構造体 電磁波伝搬制御部材付きサッシ 窓構造体及び電子機器 Astamuse




完全導体境界条件 Ykondo813 S Diary 旧パワエレ Emc日記
平面波の垂直入射 1 1 st L st v34 May21 電磁波における境界条件の使途 Region(2) Region(1) 透過 (未知) 1 1 1 1 1 1 H j E E j H ωε ωμ ∇× =表現したz 成分である.平面波で展開した半無限等方性媒質内の 界の関係式と境界Γ 1(˜x =0)上での電磁界の境界条件から,境界 Γ 1 上で,Robin 条件 1 υ d dx˜ − jcosθ i φ(0) = −j2φ 0 cosθ i at Γ 1 (10) が成立する.ここで,φ 0 は,入射電磁界の振幅であり,H 波入ンと呼ぶ.したがって,自由電荷の集団振動が電磁波と結 合した系はプラズモンポラリトンと呼ばれる.表面(また は,境界面)では,固体中でのプラズモンとは状況が異な り,表面での境界条件を満たす別の集団振動が存在するこ



新鮮な電磁波 境界 条件 最高の花の画像



電磁気学で異なる誘電体の境界条件として 電場の境界面に平行な成分が連続とありま Yahoo 知恵袋
答えだけまず書くと、電磁波(光)については普通固定端・自由端などという単純な(極端な)境界条件で反射が起こることはありません。 もっと複雑な反射をします。 とりわけ端的に言うと、反射だけでなく、同時に透過もします。 反射だけ起こるという状況はまれです。 つまり >ある媒質に光があたると反射がおきます、 という認識の時点で簡単に考えすぎというわけです。 透7.物質中の電磁波ii 71. 2誘電体間(吸収のない媒体)の境界平面における電磁波の反射と屈折 右図のように、の媒質からの媒質に角度θ1で電磁波が入射するときの反射・透過 の問題を考えよう。つまりはその境界面に平行な成分同士が連続であることが境界条件となるということだ。 もうひとつ関係式がある。 それは電束密度\(\b{D}\)、磁束密度\(\b{B}\)に対して成り立つ境界条件で、こいつらに関しては境界面において、境界面に垂直な成分同士が連続である。 \\left\{ \begin{array} ~D_{1\perp} = D_{2\perp} \\ B_{1\perp} = B_{2\perp} \end{array} ここからは実際に反射や屈折についてしっかり



2




1998 号 電磁波解析装置及び電磁波解析プログラムを記録したコンピュータ読み取り可能な記録媒体 Astamuse
1S D 2 D D t1 D n1 D n2 D2 t2 D n1D n2 = s 0 表面電荷がある場合や 電荷がない場合や の極限では D n 1 = D n 2 1 E n 1 =$ 2 E n2 電束密度の法線成分の連続性 % & D=# 1,µ ' $,µ 2 ' D&dS S =Q= # v dv upper解析条件 空気側のポート(ポート1)から電場の最大値が 1 V/m になるような TE 10 モードの電場を荷重条件として設定します。 空気・ポリエチレンの側面には全て対称境界条件を、電磁波が出力される面にはインピーダンス境界条件を設定します。 3層・垂直入射の反射と透過(電磁波・音波) 物理学 電磁気学 流体力学 POINT 散乱問題と同じように,「定常的な状態を扱う方法」と「波を追跡する方法」がある. 前者では「定常的な解+境界条件」をもとに解き,後者は「すべての反射波・透過波



光の圧力 輻射圧



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所
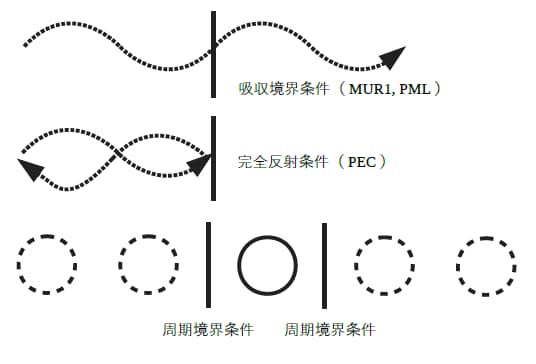
を扱うには吸収境界条件(ABC, Absorbing Boundary Condition)を用 いる必要がある。 物体からABCまでの距離は1/2波 長以上離す必要がある。 ABCは平面波をうまく吸収するよう に出来ているので、なるべく離した方 が良いが、あまり空間を大きくすると境界条件について 異なる媒質の境界(不連続部)では、マクスウェルの方程式はそのまま適用 出来ない。 →境界面に境界条件を適用 媒質内における 電磁波の伝搬 Boundary Plane Medium (ガラスなど) Region1 Region2 Region1 Region2 ε 1 , μ 1 , σ 1 ε 2 , μ 2波面の曲率 エルミート・ガウシアンビーム 分極と電場の関係 (誘電体)薄膜導波路 入射角の条件と開口数(NA) TE波とTM波 固有モードの条件 復習:TE波の全反射 スライド 79 可能なsinq の値 固有モードの波数ベクトル モードの数 固有モード(TE波)の空間



高中物理 知识点架构归纳 详细解读各个知识点间的联系 教育资讯 娱乐新闻网




新鮮な電磁波 境界 条件 最高の花の画像
電磁波による地下計測技術 第5章 電磁波の反射・散乱 54 5 電磁波の反射・透過・散乱 51 電磁界の境界条件 2つの異なる媒質の境界面においても電磁界はMaxwell の方程式で規定される物理的な条件を満足しなけ ればならない。これが電磁界の境界条件である。吸収境界条件 (Absorbing boundary condition;界条件の下で解くこと(境界値問題)である2。解 析アルゴリズムによって数値的扱いが異なり、それ ぞれ問題によって長所と短所がある。 本基礎講座では、電磁界分野の初学者のために1 次元問題3を用いて各種電磁界解析手法、特にモー



雷达波位是什么雷达的l S C X波段究竟是什么意思 都负责什么 大业商务网




电磁场与电磁波下载 Word模板 爱问共享资料
波動光学モジュールアップデート COMSOL Multiphysics ® バージョン 54 の波動光学では電磁波 (ビームエンベロープ) インターフェースを使った誘電薄膜計算のための新しい境界条件, 無反射コーティング, 鏡面様表面などの新しいが加わりました 波動光学モジュールのアップデート詳細は以下を 1 媒体の誘電率や透磁率がある面において不連続に変化する場合で,なおかつ,その不連続面に 電荷や電流が存在しない とき,この不連続面における電磁場の境界条件は次のようになります。 (1) 電場 E 、磁場 H (面電流存在しないとき) の接線成分は連続 (2) 電気変位 D 、磁束密度 B (面電荷存在しないとき) の法線成分は連続 (簡単な説明) ここでは,xy平面を不連続図2 電束密度の法線成分に対する境界条件の計算 導体中電場が存在しない→ 電束密度も存在しな い:領域1を真空、領域2を導体(図2(b)) σn = Dn = ε0En (15) 静電誘導:外部からの電場による導体の表面電荷 の誘起 12 表皮効果 導体中の変動電磁場(図3) rot




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba




電場磁場電磁波 投書 高壓電塔真的會致癌嗎 為 電磁波 闢謠 Ddmba
電磁気学III 第4講 5 E (419)0 ここでE x0は境界条件で決まる定数である。E x0は一般に複素数である。 初期条件としてE x = 0, E y ≠ 0とすれば、以下のようなEが常にy成分しかもたない解となる であろう。 (4) ここでE y0は境界条件で決まる定数で、一般に複素数である。ABC) PMLなど (a) 集中ポート (b) 導波路ポート Z 0 V (c) 平面波入射0 ³ */ I 0 V V 0 ³ E d l C I I 0 H d l 入射モード 反射モード 重み 1/2波長以上 散乱体 1/2波電磁波工学 柴田幸司 第 6 回 境界条件と伝送線路 の形となるが、これは金属境界の条件の違いや伝 搬する周波数の違いによるものである。そこで、 金属境界の構造と内部電磁界の姿体との関係を求 x



世界的本质 到底是什么 财经 参考财商报




ベクトルポテンシャルaが電磁波として矩形導波管を伝わるときに境界条 物理学 教えて Goo
磁場の境界 アンペールの法則の積分形 ・ ∫ C H ( r, t) ・ d r = 0 を、電場の境界を考えたときと同じ長方形の外周を積分範囲と設定することで、磁束密度の境界条件も求まる。 ただし、電流と時間変化する外部電場が存在しない ( i = 0, ∂ D ∂ t = 0 )とする。 ・ ・ ∫ C H ( r, t) ・ d r = ( H 1 − H 2) ・ t l アンペールの法則よりこれが0になるということだから、次の関係が求まる。 H 1 = H 2完全導体中では電磁波は存在できないので,領域iiの総合電界e ii =0となる。式(8)と式(10)および境界条件より, 境界面(x=0面)で電界の接線成分(y成分)が等しいと置くと次式を得る。 境界条件も、ディリクレ境界条件と吸収境界条件の二つを与えられるようにしよう。 また、媒質の位置やパラメータも与えられるようにする。 これで結構面白い波の波形が得られる。 32 Yee格子 まず、Yee格子を作っていこう。




看不见的电磁波甘本祓著中国大百科出版社 摘要书评试读 京东图书



佚名 文革中的婚礼和证书 Cnd刊物和论坛
Minoru TANAKA (Osaka Univ) 25 誘電体の境界条件 • 2種類の誘電体,誘電体1と誘電体2,の境界面を考える.それ ぞれの誘電率をε1,ε2 とし,境界面に電荷はないものとする. 境界面を囲む微小なうすい円筒(底面積 ΔS) を考えて,ガウスの法則を適用すると, (1) D(r)dS =0132 電磁波 169 132 電磁波 Amp`ereの法則の拡張,すなわち,変位電流が磁場をつくることは理論的考察に基づいた仮 定であり,実験で検証しなければならない。 Maxwellは,偏微分方程式を組み合わせると電場と磁場に関する波動方程式が導かれるこ とを示した。波動方程式の解は電場と磁場の時




Fdtd法の解説ページをリニューアルしました 株式会社科学技術研究所




逆l形アンテナ アース理論実証 その12 誘電体 5 磁界の強さhの境界条件 Jo3krpの独り言




什么是emc工程师 Emc Wiki 致力于电磁兼容技术



科学道德与学风 21雨课堂答案 第4章 Chow 的博客 Csdn博客



2




看不见的光 从红外线到x光 电磁波发现趣史 摘要书评试读 京东图书



引力与电磁波的爱恨情仇 知乎
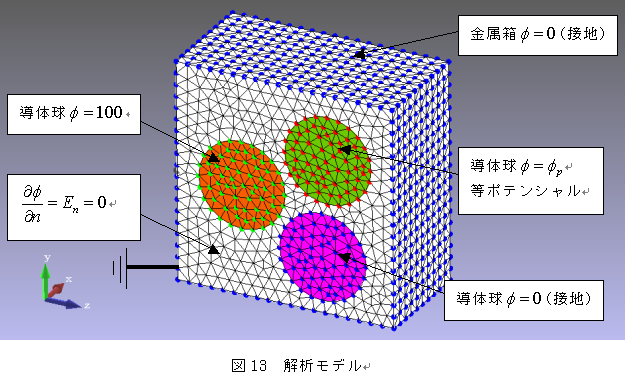



その12 電磁場の境界条件について 株式会社フォトン
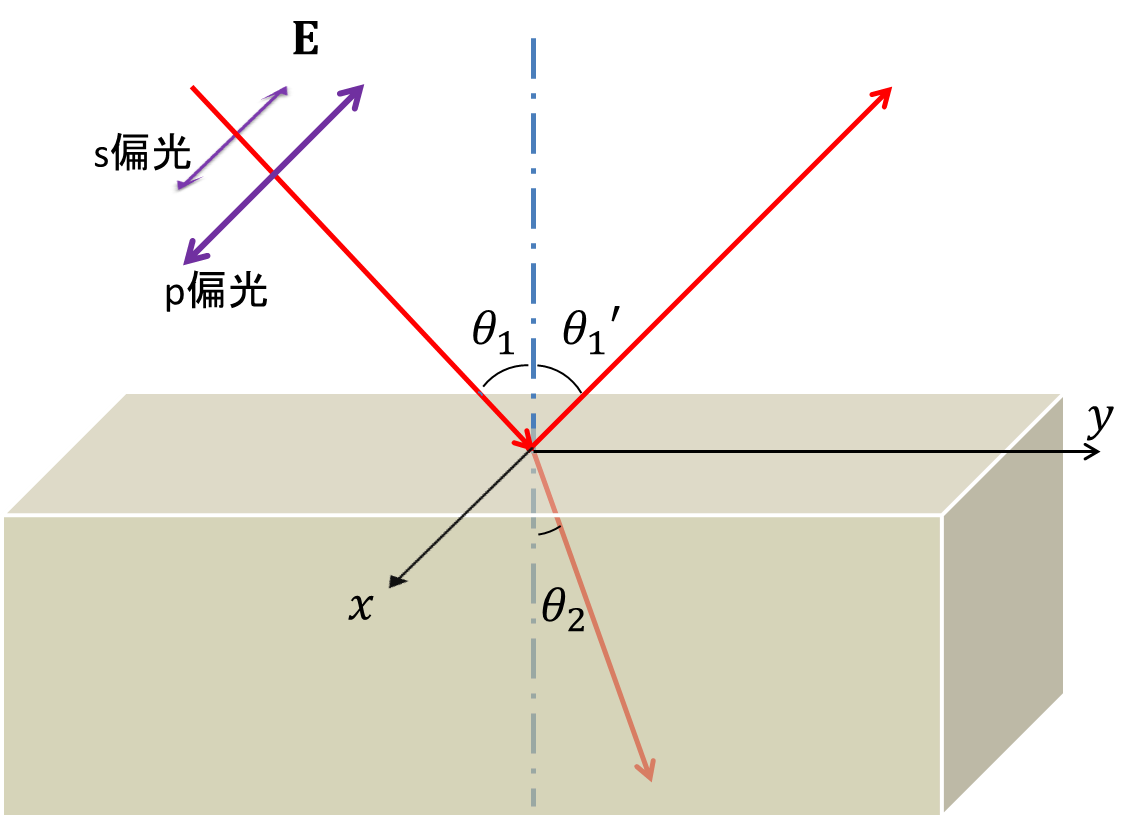



物理とか 偏光と境界条件 反射 屈折の法則




電場磁場電磁波科學人雜誌 Cxyg



1



電磁波の完全導体の境界条件についての質問です 境界面で Yahoo 知恵袋
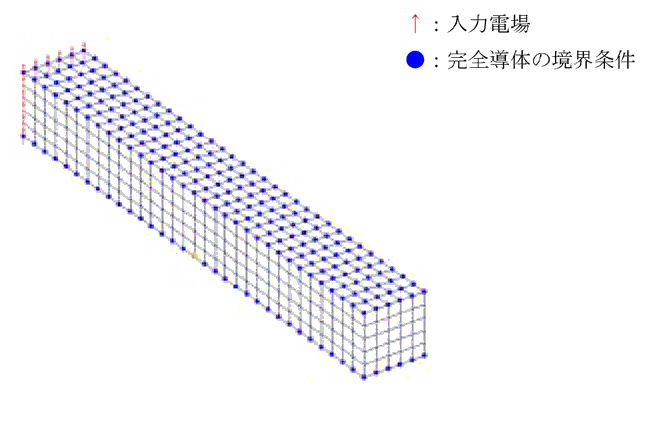



スライドインタフェースを用いた平行平板内の電磁波解析 株式会社フォトン




射频微波 高频仿真技能修炼纪要分享 下 射频 微波 与非网



精神可独立于肉体之外存在么 头条问答




地球暴露了吗 比邻星传来无线电信号 外星文明或在盯着地球 行星 宇宙空间 电磁波 网易订阅



如果人类建立了月球基地和火星基地 那么如何保持和地球的关系 时习社区




新鮮な電磁波 境界 条件 最高の花の画像
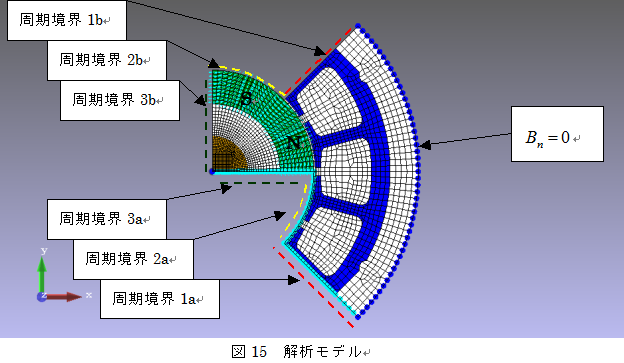



その12 電磁場の境界条件について 株式会社フォトン



9章 反射と屈折の法則



2




電磁気学 Electromagnetics 6 5講義分 電磁波の反射と透過 山田 博仁 Ppt Download




境界条件 ムラタソフトウェアブログ



改运就是扬升频率 意识




電場磁場電磁波科學人雜誌 Cxyg



Ppt 電磁気学 C Powerpoint Presentation Free Download Id
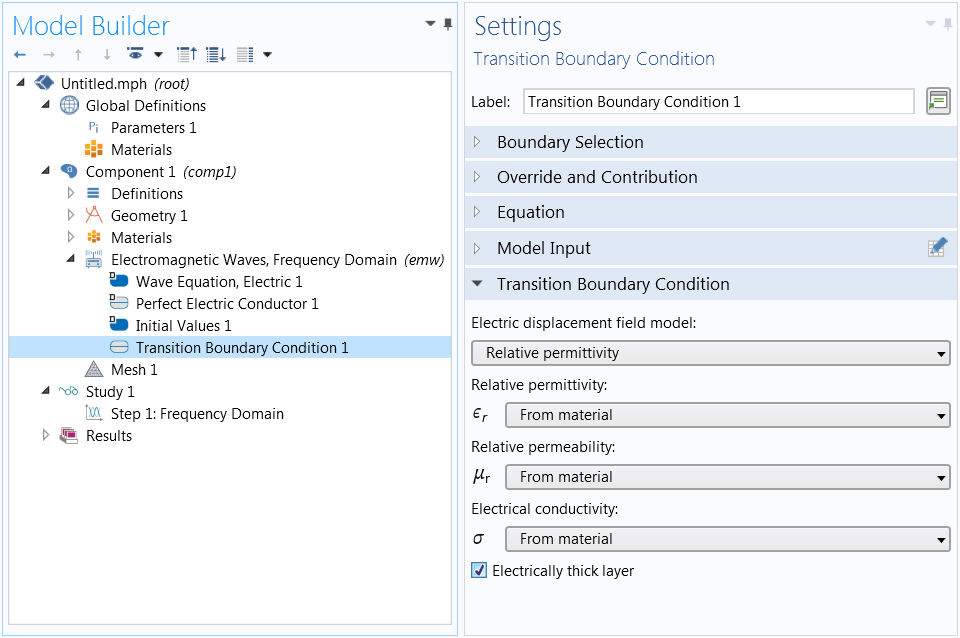



Wave Optics Module Updates Comsol 5 4 Release Highlights
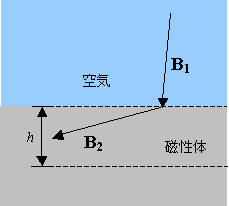



電磁気学における磁性体の境界条件1




電磁気学c Electromagnetics C 5 22講義分 電磁波の反射と透過 山田 博仁 Ppt Download



庞加莱 最后一个什么都会的科学家丨贤说八道 返朴 财新博客 财新网



電磁波の境界条件について Http Cobalt Cneas Toh Yahoo 知恵袋




波動光学モジュール Comsol 5 1 リリースハイライト




3層 垂直入射の反射と透過 電磁波 音波 Notes Jp




逆l形アンテナ アース理論実証 その13 誘電体 6 電磁波の 電界と磁界の境界条件の関連性 Jo3krpの独り言




解析シミュレーションソフトfemtet のバージョンアップについて 村田製作所




西天雄文堂 Home Facebook




某科学的超电磁炮ss3下 5 8章 完



2




日本yahoo拍賣 樂淘letao代購代標第一品牌 振動及び波動末岡清一昭和23年 単振動 多自由度の振動 連続体の振動 電気振動 回析 干渉 音波 水波 電磁波 物質波



電磁波の伝播




某科学的超电磁炮ss3下 5 8章 完




计算机电磁辐射泄密 是目前防窃密的薄弱环节 博学科技网



山中地下2400米 建在四川的世界最深地下实验室 在研究什么 全网搜




電界と電束密度の境界条件 Cupuasu クプアス
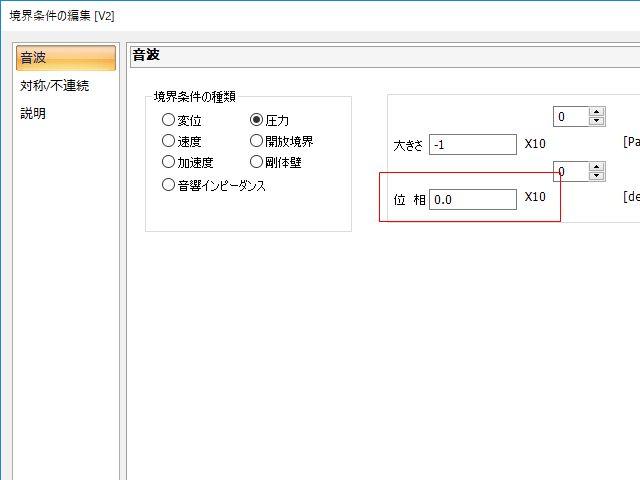



境界条件 ムラタソフトウェアブログ
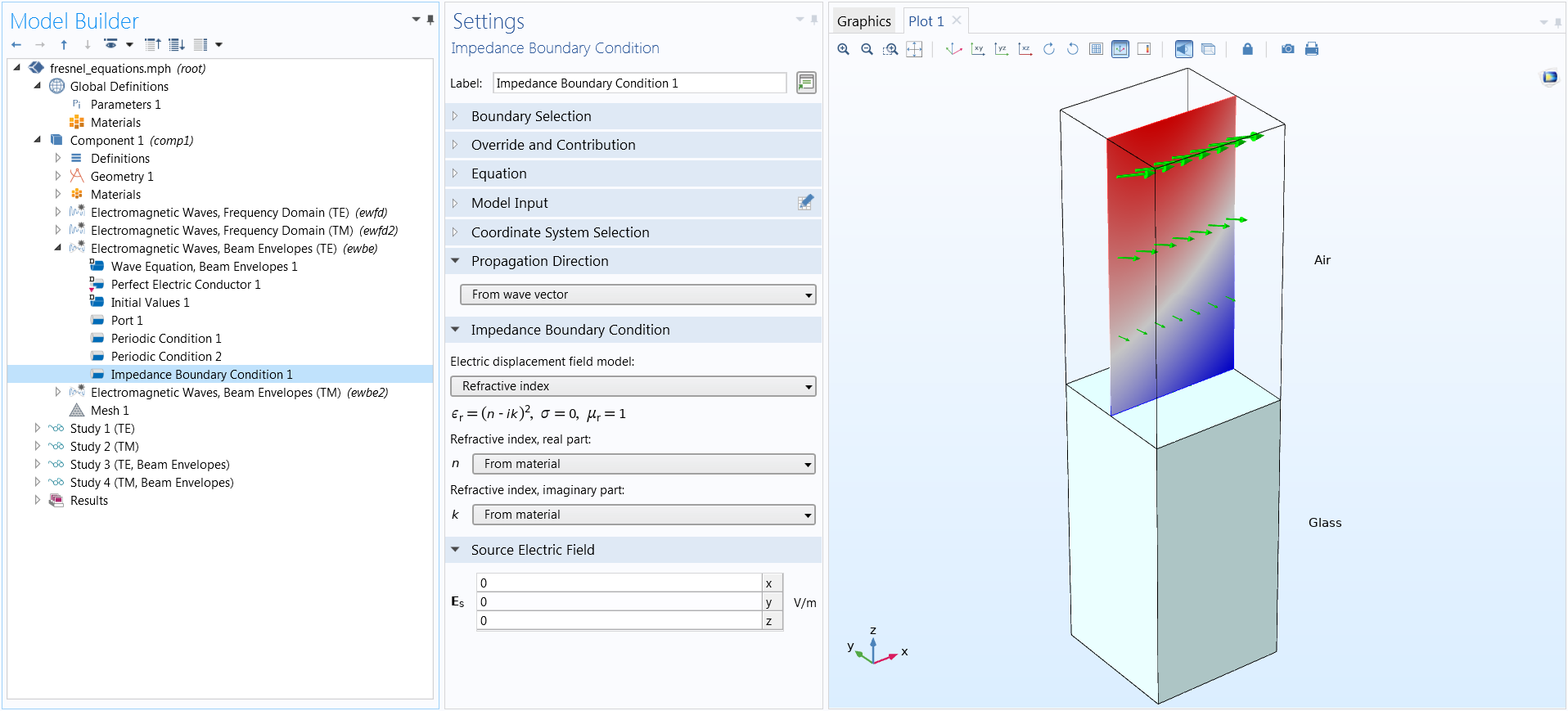



Wave Optics Module Updates Comsol 5 4 Release Highlights



Accwww2 Kek Jp



电磁场下载 Ppt模板 爱问共享资料



新鮮な電磁波 境界 条件 最高の花の画像



高端窗膜制造的三种 神 器 自由微信 Freewechat




Fdtd法によるアンテナ 電磁波解析 出版物 Tech Seminar Jp



头条问答 某大学教授认为双缝干涉实验是假的 你怎么看 雄途科技1的回答 0赞



2
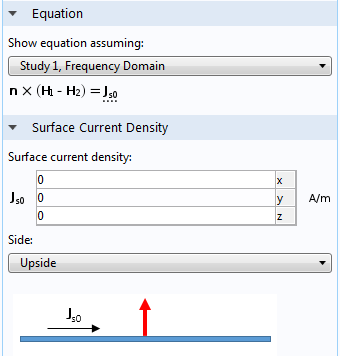



波動光学モジュール Comsol 5 1 リリースハイライト
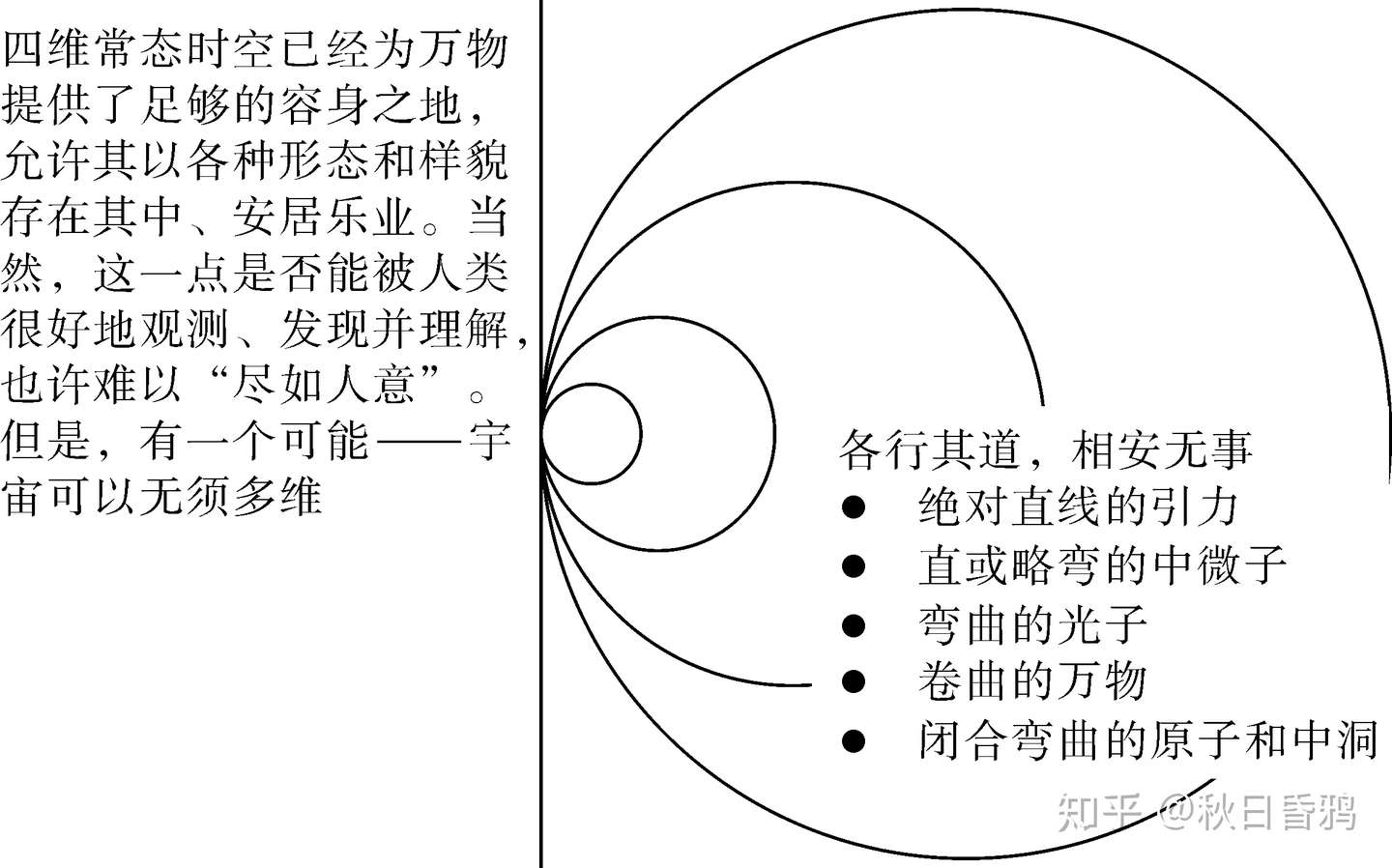



引力与电磁波的爱恨情仇 知乎



異なる媒質の境界における電磁波と電子波 2 2 電磁波に対する透過係数と反射係数の導出




高等学校教材 工程电磁场与电磁波 摘要书评试读 京东图书



改运就是扬升频率 意识




计算机电磁辐射泄密 是目前防窃密的薄弱环节 博学科技网




Pdf 卫星遥感影像处理技术分析




スライドインタフェースを用いた導波管の電磁波解析 株式会社フォトン




05 号 電磁界解析装置 電磁界解析方法および電磁界解析プログラム Astamuse




Literature 文学 高大伟david Cowhig S Translation Blog



2




唐吉诃德 多弗朗明哥 搜狗百科



初中生看阅兵要看本质阅兵式的中考考点大汇整 组图



买多优选医之本吸地气少生病理疗鞋的原理是什么 价格多少钱 南方科技网




战场伪装加重 战争迷雾



電磁気の境界条件 の問題について質問です 画像の問題で 電場と電束 Yahoo 知恵袋
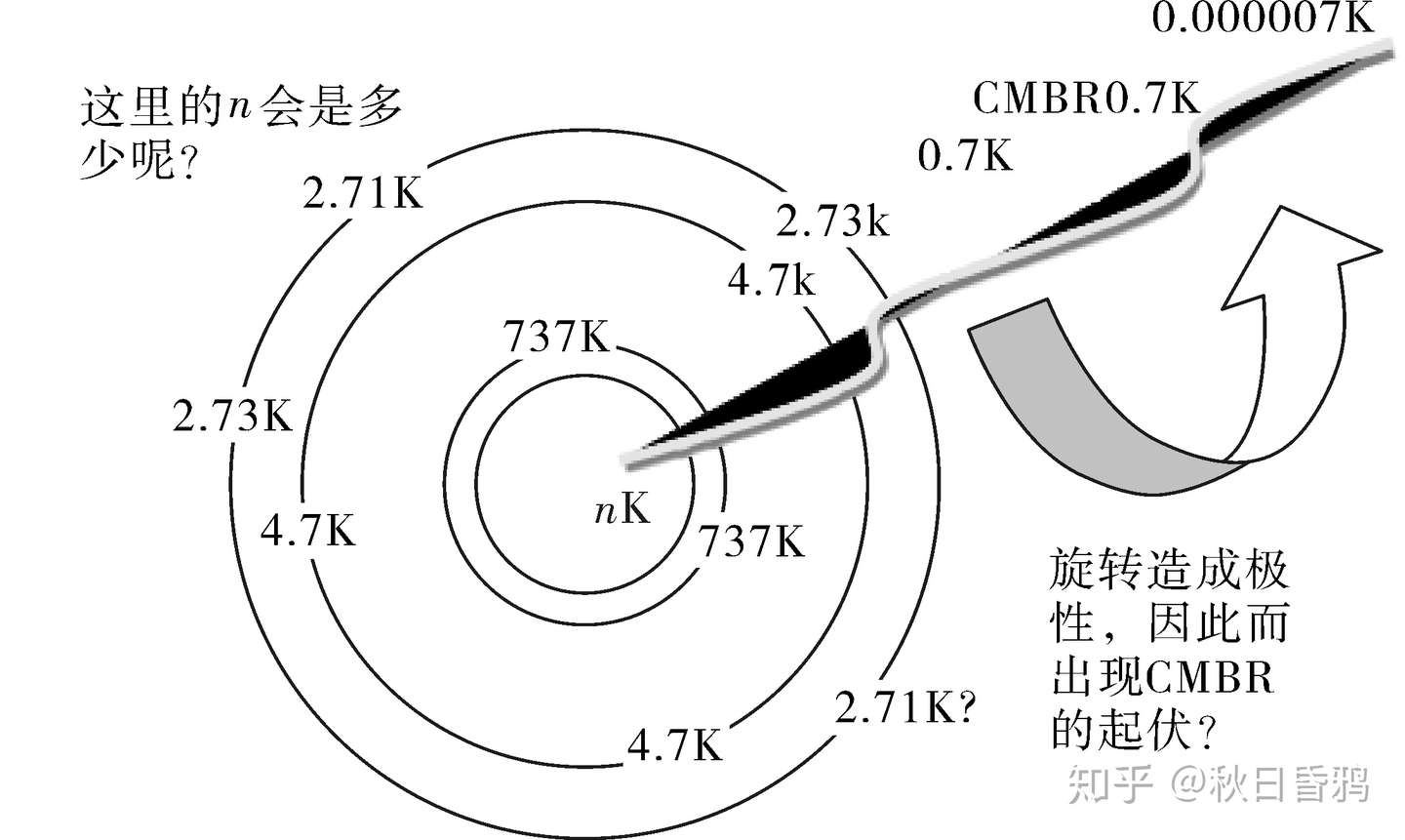



引力与电磁波的爱恨情仇 知乎
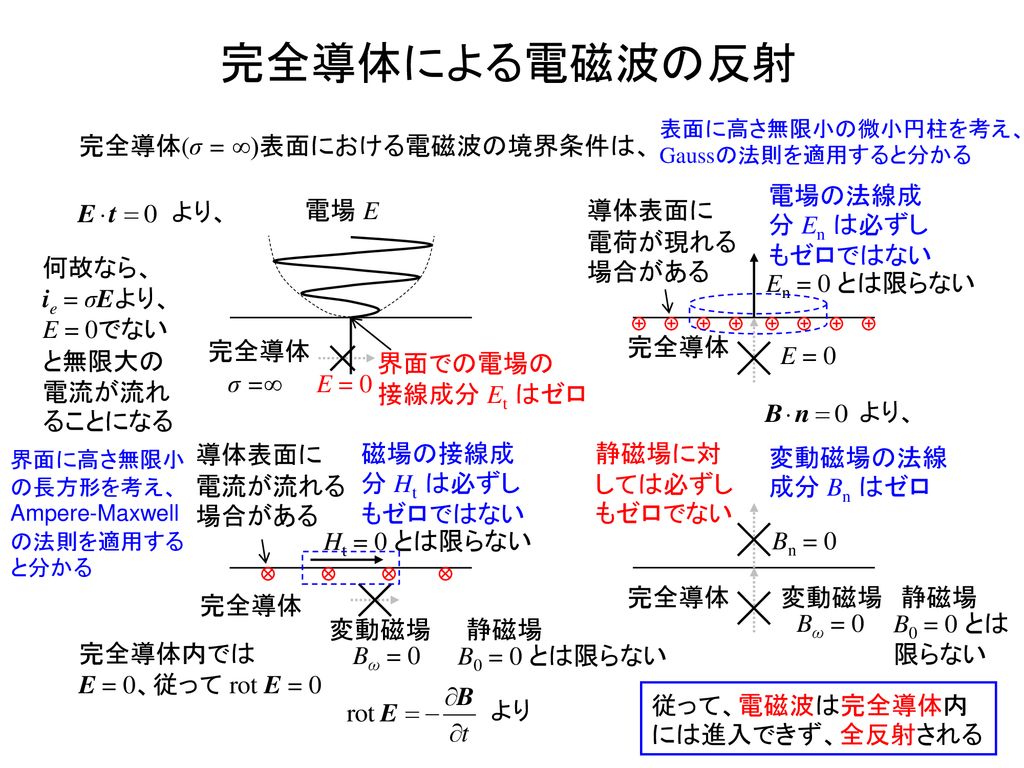



電磁気学 Electromagnetics 6 講義分 共振器と導波路 山田 博仁 Ppt Download




新鮮な電磁波 境界 条件 最高の花の画像




電場磁場電磁波科學人雜誌 Cxyg



フレネルの式 Emanの電磁気学



维生素c Vit C 第3页 成长医学博士博客



2




气功 特异功能及其他 原載 中國青年 1987年10月 Mzi
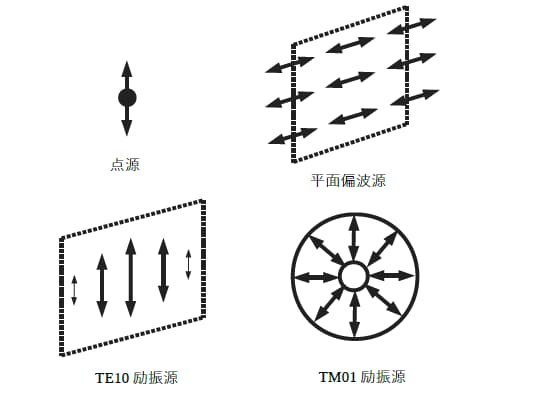



励振源 境界条件 収束判定 解析の実効値 株式会社科学技術研究所



改运就是扬升频率 意识




Wo19 号 電磁波伝搬制御部材 電磁波伝搬制御構造体 電磁波伝搬制御部材付きサッシ 窓構造体及び電子機器 Astamuse
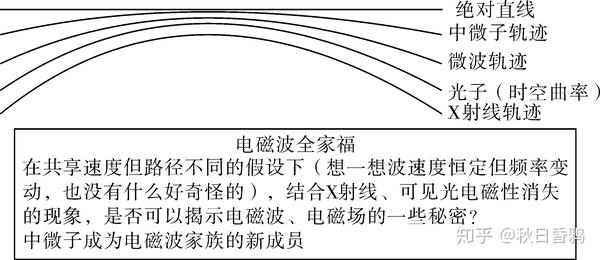



引力与电磁波的爱恨情仇 知乎



0 件のコメント:
コメントを投稿